My Friends,
@Fighter, I have done a little research and see some of N.E. Zaev's work. Yes a Heat Exchanger of sorts, a very confusing exchange of Energy into Coils and Capacitors as we would normally understand it:

Ref: http://jnaudin.online.fr/html/nzaeexp.htm
I remember reading this years ago, I did not recall the name: from Nikolay Zaev.
I have done a lot of research in this area, but can not prove it, and can not find a way to further understand it, however in saying this, I have a feeling, what YoElMiCrO is saying is close and maybe right! I think we need to think of this in another way however.
Quote from my attached pdf above:
As we know, in usual transformer BH loop traversed counter-clockwise and loop’s area corresponds to energy loss in transformer core. But if we manage to create such device where BH curve traversed clockwise, area of the loop will represent an energy gain.
The plot forms an ellipse whose area represents the energy lost per cycle. Note the area is traversed anti-clockwise.
Of interest to OU researchers is the concept of negative resistance, since this represents a source of energy rather than a sink. The next figure shows the Φ v I plot for an inductor shunted by a negative resistor.
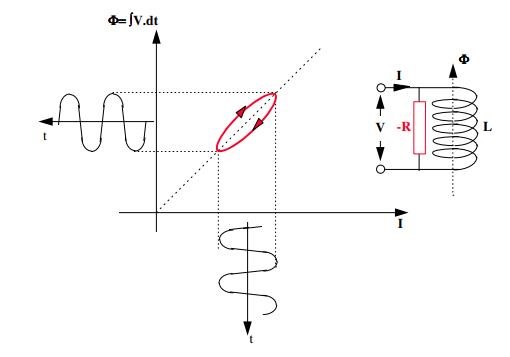
Figure 5. Φ v. I plot for negative resistor
Ref: PDF Document 'h2e' Image from 'A New Look at the Bearden MEG © Smudge, May 2014 Smudge', aka Cyril Smith.
Now, some of this makes sense to me, some of it, but not all of it. So I cant say this is how its done! I have researched working at the knee of the BH Curve before, but again, even though knowing about this area where there may be some advantage working, I can not say for sure this is what is required and what is needed.
2. Synthesizing a Clockwise Φ v. I Loop
It is known that, by the use of short-circuited coils, it is possible to divert flux from a magnetic material. Thus it may be possible to synthesize the clockwise loop by stitching together two different characteristics. Consider the following typical Φ v. I characteristic for a saturating material.

Figure 6. Φ v. I plot for saturating material
If we could arrange for flux within a coil to be positive-going while also going over the positive saturation knee, then when negative-going it does not trace its original steps, but passes over the negative saturation knee, we would get the combined characteristic we desire. The following section is devoted to this possibility. First consider a magnetic core having two coils connected in series aiding, yielding an inductance L.
Ref: A New Look at the Bearden MEG - By Ciryl Smith aka Smudge
I would recommend more research in this area! In my following experiment, perhaps the loop here may have some relevance?
Cyril Smiths document: A New Look at the Bearden MEG, is attached below.
@YoElMiCrO - I also am looking forward to seeing more of your experiments and results! A greater overall understanding is what I strive for! I appreaciate your input here, Thank You! I found this interesting:
One way to cool a gas is as follows. First compress it isothermally. This means compress it in a vessel that isn’t insulated, and wait for the gas to lose any heat that is generated so that it returns to room temperature. Then insulate the vessel and allow the gas to expand adiabatically. We could call this cooling by adiabatic decompression.
You can cool a rubber band as follows. First stretch it isothermally. That means, stretch it slowly, so that it has lots of time to lose any heat that is generated. Then, suddenly destretch it, and before it has time to gain any heat from its surrounding, measure its temperature by immediately holding it up to your lips. You will find that it has cooled by adiabatic de-stretching. (If you stretch the band quickly (i.e. adiabatically) and immediately hold it up to your lips, you will find that it is hot. BUT ... before you try that experiment, close your eyes tightly. You don’t want the stretched elastic band to break and hit you in the eye. Believe me, you do not want that to happen.)
The method of adiabatic demagnetization has been used to obtain extremely low temperatures. A sample of a paramagnetic salt (such as cerium magnesium nitrate), already cooled to low temperatures by other means, is magnetized isothermally. The sample is often suspended in an atmosphere of helium, which can conduct away any heat that is produced, and hence keeps the process isothermal. It is then insulated (by pumping out the helium) and suddenly and adiabatically demagnetized. This process of isothermal magnetization followed by adiabatic demagnetization can be repeated over and over again. Temperatures close to 0 K have been reached in this manner. You could actually reach a temperature of absolute zero if you did this an infinite number of times – but not for any fewer.
In the analysis that follows, I shall have to assume that you are familiar with the concepts of B, H, magnetic moment and magnetization from electricity and magnetism.
In brief, the magnetic dipole moment pm of a sample is the maximum torque it experiences in unit field B. That is, the torque is given by . τ = pm × B The magnetization M of a specimen is defined by ). ( B = µH = µ0 H + M The magnetization is also equal to the magnetic moment per unit volume.
Now consider the following.
If the tension in an elastic string is F, the work done on the string when its length is increased by dx is F dx.
If the pressure of a gas is P, the work done on the gas when its volume is increased by dV is −P dV.
Ref: http://astrowww.phys.uvic.ca/~tatum/thermod/thermod15.pdf
Again, I just want to say, do your own research here, I agree with what YoElMiCrO has said, I am partly in agreeance with some of the above, but not all of it! Come to your own educated conclusions!
Stay safe and well everyone!












